A DC generator converts mechanical energy into electrical energy using the principle of electromagnetic induction. When the armature rotates inside a magnetic field, an electromotive force (EMF) is induced in its conductors. This EMF is the reason current flows through the circuit. In this topic, we will learn how to derive the EMF equation of DC generator in a simple and easy way.
Let,
P=Number of poles
Z = Total number of armature conductors
ϕ = flux per pole in weber
N = Speed of armature in r.p.m. (revolutions per minute)
A = Number of parallel paths (A = 2 for Wave winding and A = P for Lap winding)
Eg = EMF (Electro Motive Force) of the generator = EMF per parallel path [Explanation]
First, we need to find the EMF generated per conductor.
The total flux linked with one conductor during one full revolution of the armature.
Flux cut per conductor per revolution = P ϕ
$$ d\phi = P\phi \text{ Webers} \quad \text{——— (i)} $$
[Here, dϕ just means a small part of the total magnetic flux being cut by the conductor.]
The time required for one full rotation of the conductor.
$$ dt = \frac{60}{N} \text{ seconds} \quad \text{——— (ii)} $$
Now, from Faraday’s law of electromagnetic induction, we know that
$$ \text {emf (e)} = \text{Number of Conductors} \times \frac{d\phi}{dt} $$
Here, for one conductor
$$ e = 1 \times \frac{d\phi}{dt} $$
Hence, emf generated per conductor,
$$ e = \frac{d\phi}{dt} $$
Substituting from equations (i) and (ii)
$$ e = \frac{P\phi}{(60/N)} $$
$$ = \frac{P\phi N}{60} \text{ volts} $$
Next, we need to find the total EMF generated by all the conductors.
Total EMF generated by all the conductors (Eg)
= emf per parallel path
= emf per conductor x No. of conductors in series per parallel path [Explanation]
$$ = \frac{P\phi N}{60} \times \frac{Z}{A} $$
$$ E_g = \frac{P\phi ZN}{60A} \text{ volts}$$
This is the derivation of the EMF equation of DC generator or the back EMF equation for a DC motor.
Why is the EMF of the generator = emf per parallel path= emf per conductor x No of conductors in series per parallel path?
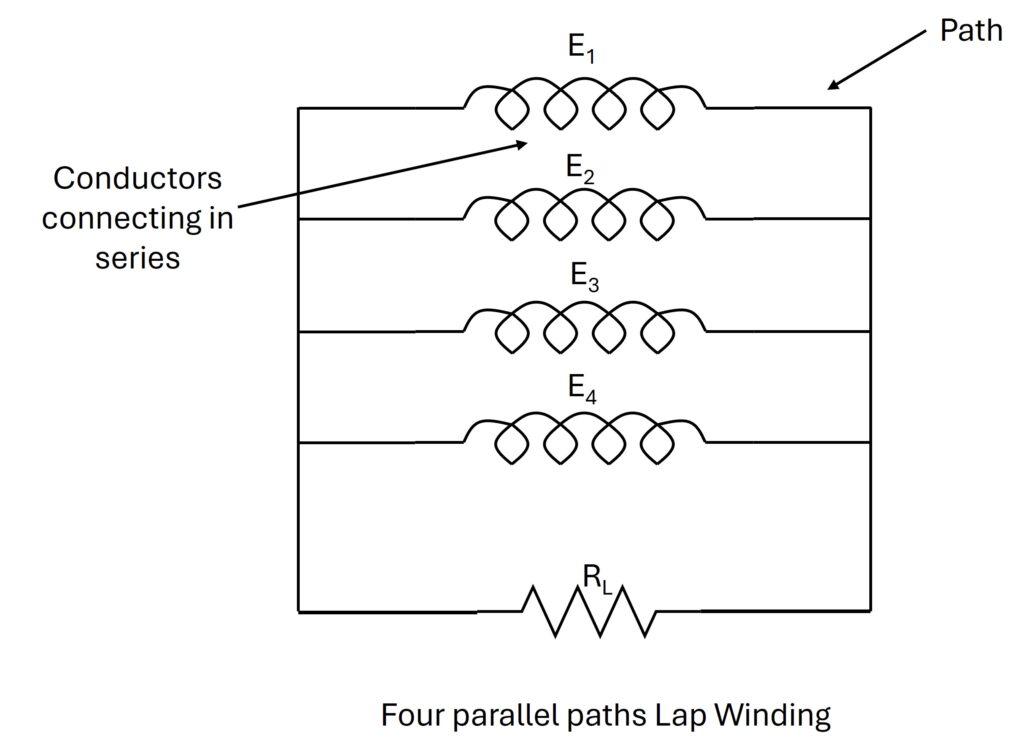
In the armature, conductors are divided into parallel paths. All conductors in one path are in series, so their EMFs add up. All such paths are connected in parallel, so the same EMF appears across each path. Thus, the total EMF of the generator is equal to the EMF generated in any one parallel path.
Here each path emf, E1 = E2 = E3 = E4 = Eg
FAQs on EMF Equation of DC Generator
1. What is the EMF equation of a DC generator?
The EMF equation of a DC generator is:
$$ E_g = \frac{P\phi ZN}{60A} \text{ volts}$$
2. How can we increase the EMF of a DC generator?
You can increase the generated EMF by:
- Increasing the magnetic flux (ϕ)
- Increasing the speed (N)
- Increasing the number of poles (P) or armature conductors (Z)
3. What happens if the speed of the DC generator increases?
If the speed (N) increases, the generated EMF (Eg) also increases proportionally, because Eg ∝ N.