The transient response of RC circuit describes how the voltage and current change with time when a sudden input, such as connecting or disconnecting a DC source, is applied. Because a resistor and capacitor store and release energy at different rates, the circuit does not reach its final value instantly. Instead, it follows an exponential rise or fall. Understanding this behaviour helps in analysing charging and discharging of capacitors, time constant, and step response, which are essential for electronics, filters, and timing applications.
What are Electrical Transients?
Electrical transients are sudden, short-lived surges of energy that appear in power lines or data/communication lines. They happen for a brief time and then die out.
What is Transient Response?
When we apply an input (like a DC voltage) to a circuit, the output (voltage or current) does not jump to its final value instantly. It takes some time to settle. The behaviour during this settling period is called the transient response.
RC Circuit Transient (Charging and Discharging)
An RC transient happens when a capacitor charges or discharges through a resistor. During charging, the capacitor starts at zero volts and slowly rises toward the battery voltage. The current is strong at the beginning and then becomes weaker as the capacitor fills up, just like a water tank filling through a narrow pipe.
During discharging, the capacitor releases its stored energy through the resistor. Its voltage slowly falls to zero, dropping quickly at first and then more slowly as it empties, like a tank releasing water through the same pipe.
Now, we will study the transient response of RC Circuit, using a simple series R–C circuit connected to a DC source. This is a first-order circuit and is perfect for learning the basics of transient analysis.
Let,
R = resistance (ohms, Ω)
C = capacitance (farads, F)
V = DC source voltage (volts, V)
Vc = capacitor voltage at time t
VR = resistor voltage
i = circuit current at time t
Charging a capacitor
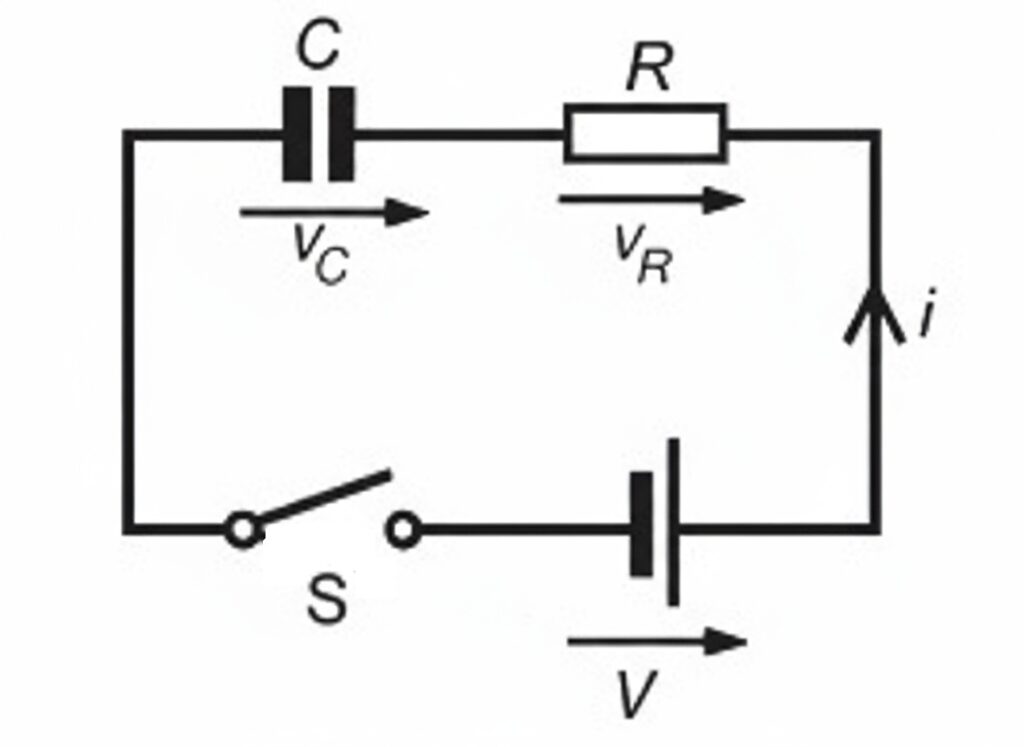
The circuit diagram for a series-connected C–R circuit is shown in Figure. When switch S is closed, then by Kirchhoff’s voltage law:
$$V=v_c+v_R {\text ———- (i)}$$
Where VC is the voltage across the capacitor and VR across the resistor.
The current in the circuit is
$$i=C\frac{dv_c}{dt}$$
Voltage across the resistor
$$v_R=iR=RC\frac{dv_c}{dt}{\text ———- (ii)}$$
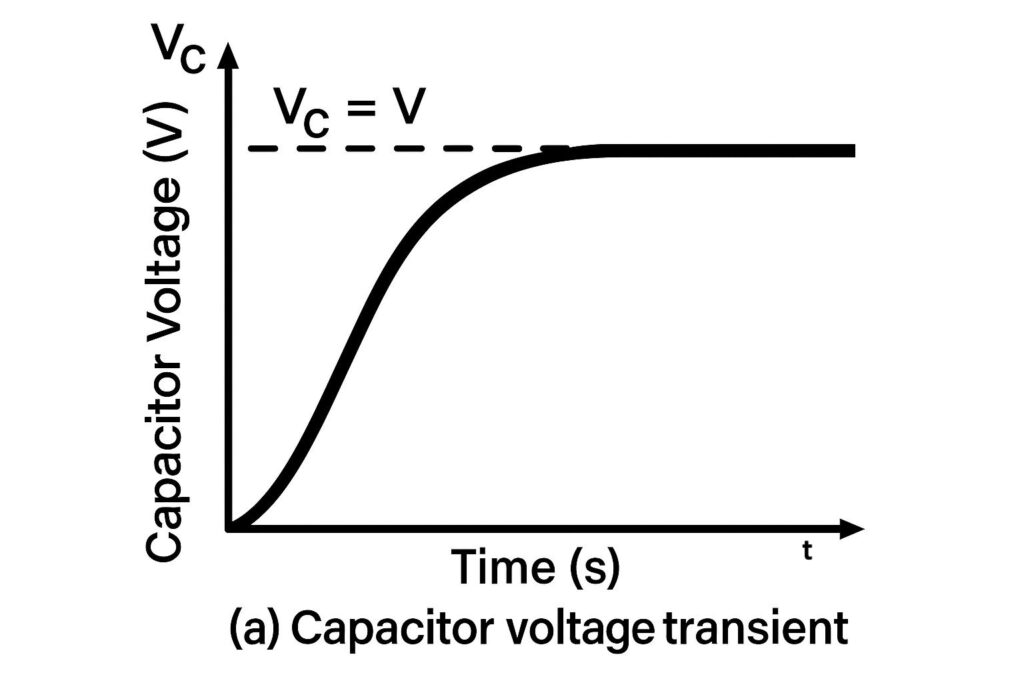
Capacitor Voltage Transient
By substituting the value of VR into the equation (i), we get:
$$V=v_c+v_R$$
$$V= v_c + RC\frac{dv_c}{dt}$$
$$\frac{dv_c}{dt}=\frac{V-v_c}{RC}$$
$$\frac{dv_c}{V-v_c}=\frac{dt}{RC}$$
Integrating both sides, we get
$$\int\frac{dv_c}{v-v_c}=\int\frac{dt}{RC}$$
$$-\ln(V-v_c)=\frac{t}{RC}+k$$
where k is the arbitrary constant of integration.
When time t=0, vc=0, hence $$-\ln V=k$$
Thus, From equ. (iv)
$$-\ln(V-v_c)=-\ln V+\frac{t}{RC}$$
By laws of logarithms
$$\ln\frac{V}{V-V_c}=\frac{t}{RC}$$
$$\frac{V}{V-V_c}=e^\frac{t}{RC}$$
$$V-v_c=Ve^{-\frac{t}{RC}}$$
$$v_c=V(1-e^{-\frac{t}{RC}})$$
In the above equation, RC is called the time constant, which is denoted by τ.
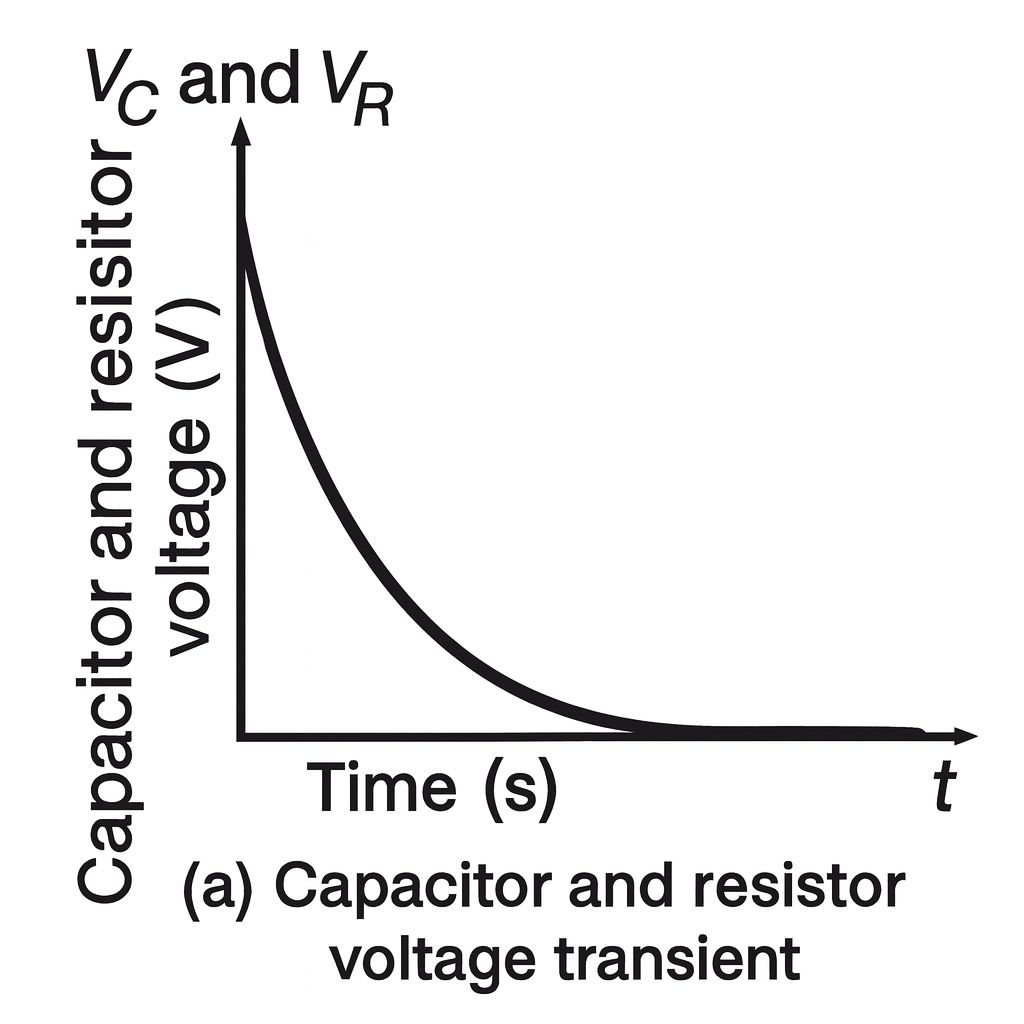
This is an exponential growth curve, as shown in figure (a).
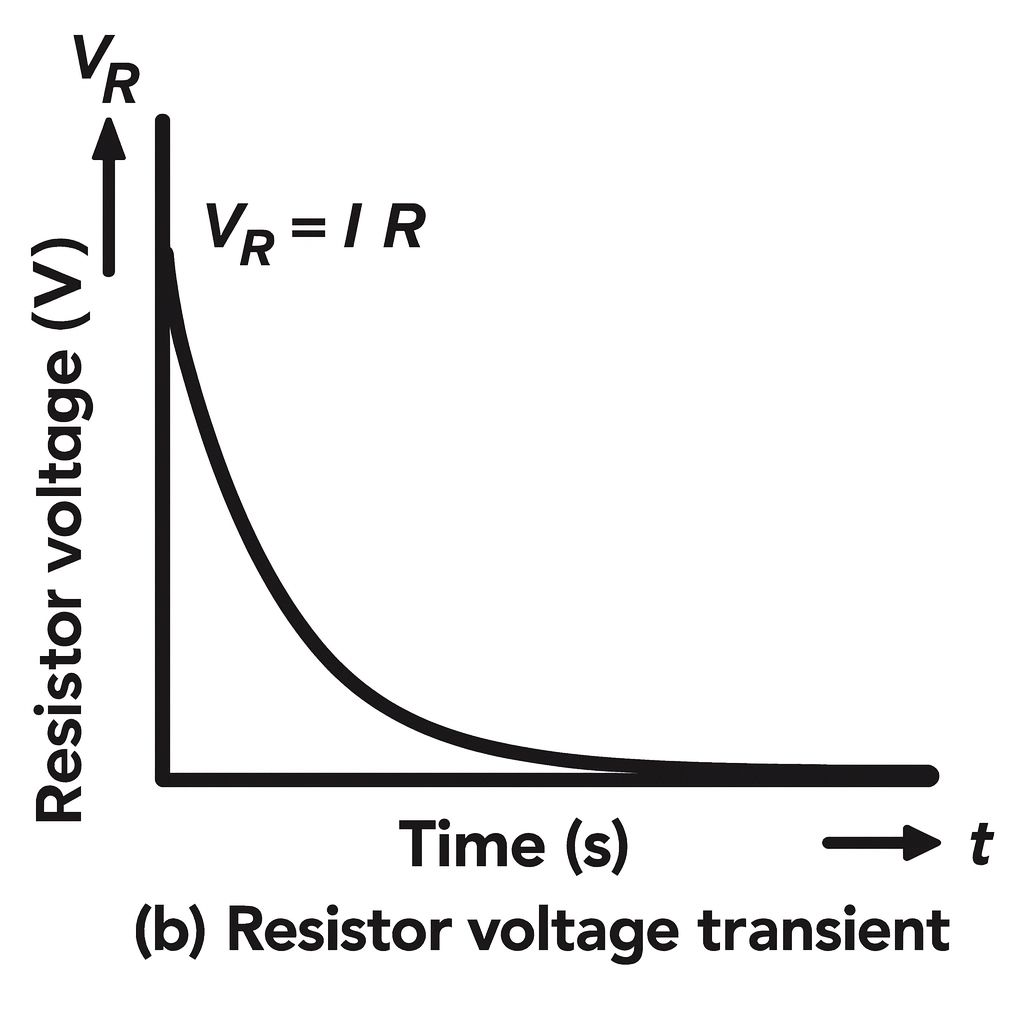
Resistor Voltage Transient
From equation (i),
$$v_R=V-v_c$$
$$v_R=V-V(1-e^{-\frac{t}{RC}})$$
$$v_R=Ve^{-\frac{t}{RC}}$$
This is an exponential decay curve, as shown in Figure (b).
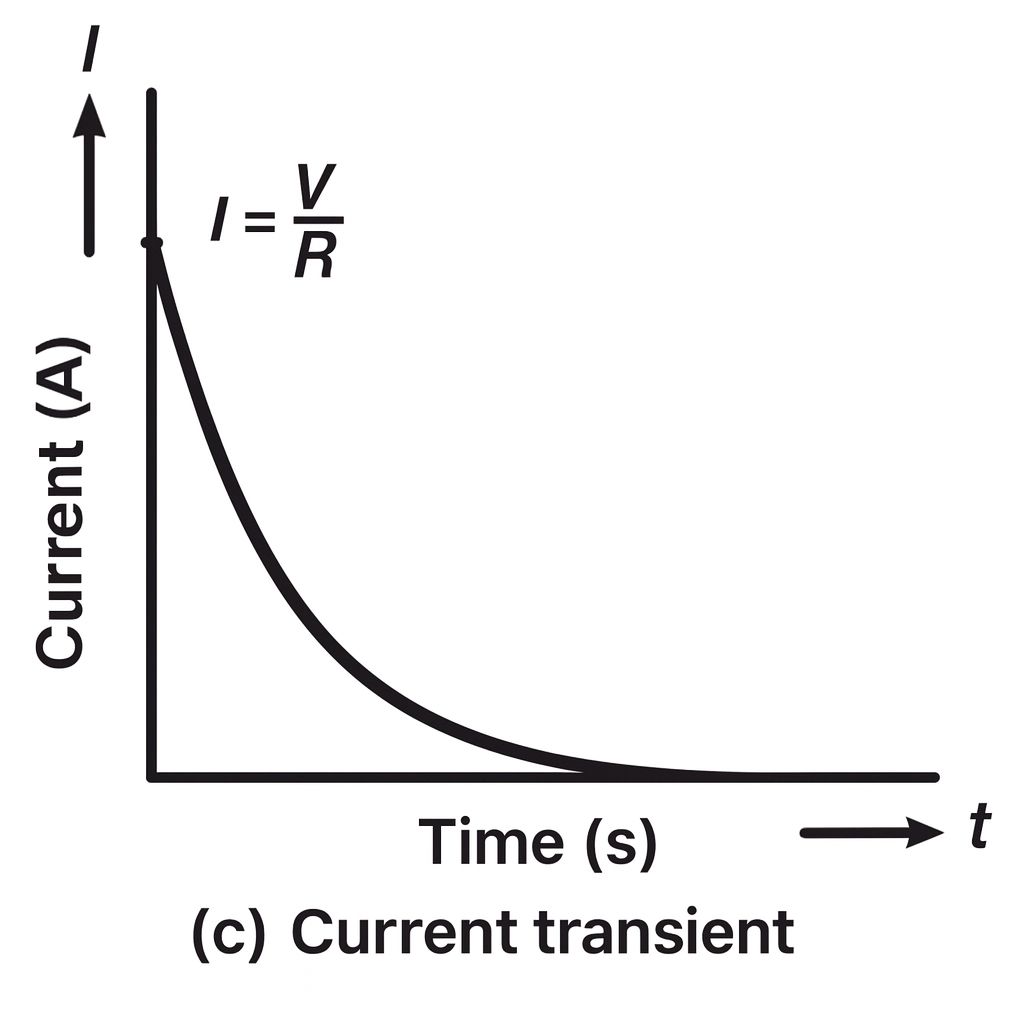
Current Transient
In the circuit, current
$$i=C\frac{dv_c}{dt}$$
$$i=C\left[\frac{d}{dt}V(1-e^{-\frac{t}{RC}})\right]$$
$$i=C\left[0-V\left(-\frac{1}{RC}\right)e^{-\frac{t}{RC}}\right]$$
$$i=\frac{CV}{RC}e^{-\frac{t}{RC}}$$
$$i=\frac{V}{R}e^{-\frac{t}{RC}}$$
where V/R is the steady-state current, I.
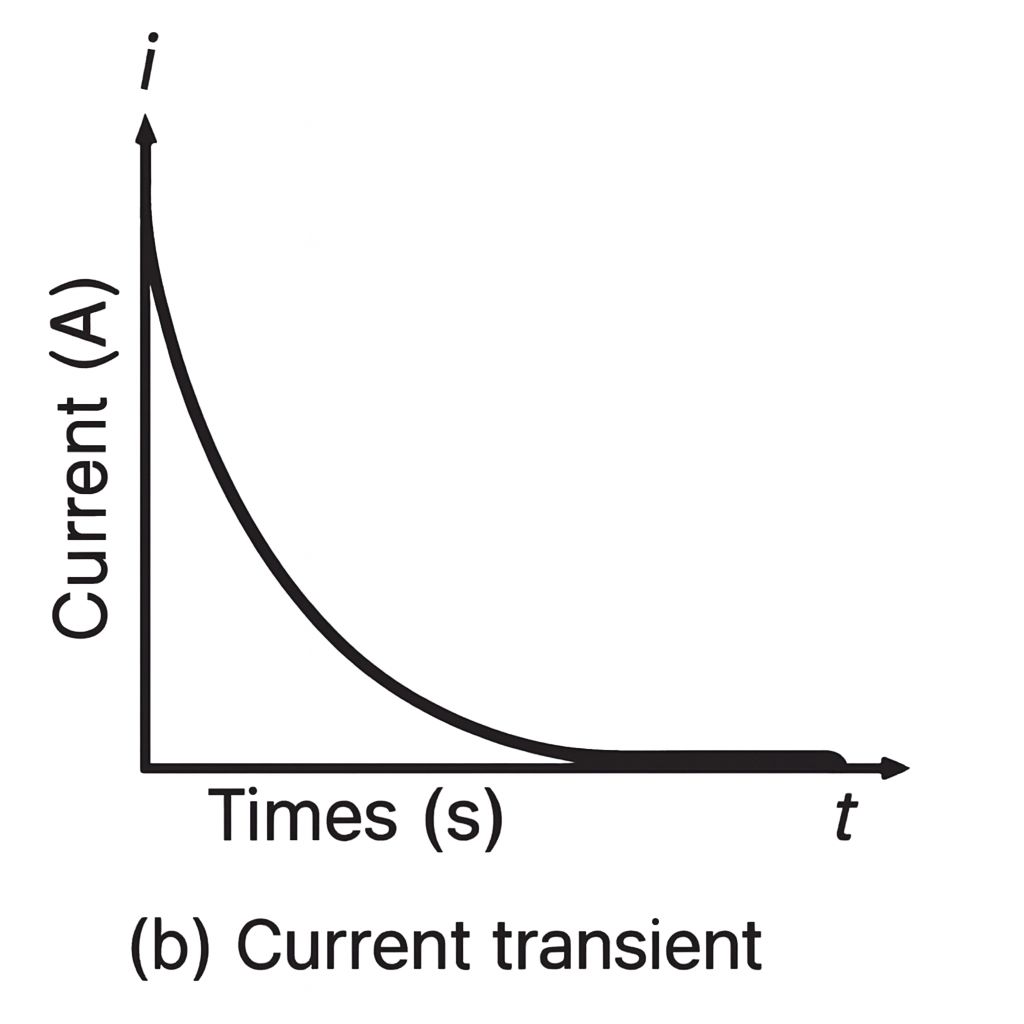
This is an exponential decay curve, as shown in Figure (c).
After a period of time it can be determined from equations that the voltage across the capacitor, vc, attains the value V, the supply voltage; the resistor voltage, vR, and current i both decay to zero.
Discharging a capacitor
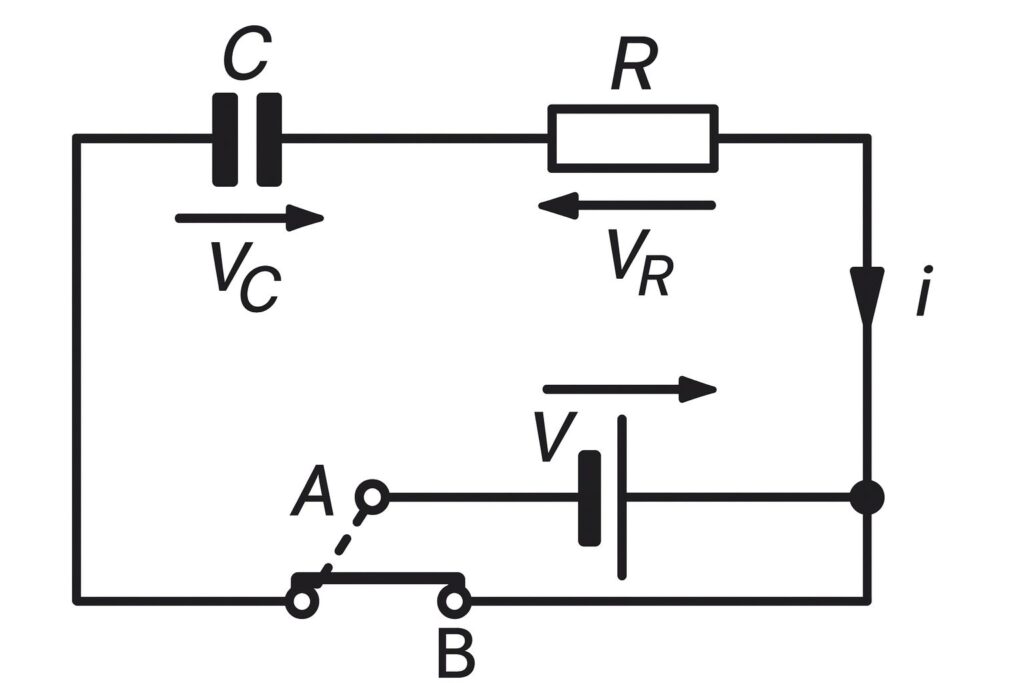
If, after a period of time, the step input voltage V applied to the circuit of Figure is suddenly removed by opening the switch, then from equation (i):
$$v_R + v_c = 0$$
Or, from equation (ii),
$$RC\frac{dv_c}{dt} + v_c = 0$$
$$\frac{dv_c}{dt} = -\frac{v_c}{RC}$$
$$\frac{dv_c}{v_c} = -\frac{dt}{RC}$$
Integrating both sides gives:
$$\int\frac{dv_c}{v_c}=-\int\frac{dt}{RC}$$
$$\ln v_c = -\frac{t}{RC} + k$$
where k is an arbitrary constant.
At time t = 0 (instant of opening the switch), vc= V. Substituting t = 0 and vc = V in the equation gives:
$$\ln V = k$$
Hence, the equation becomes:
$$\ln v_c = -\frac{t}{RC} + \ln V$$
or
$$\ln v_c – \ln V = -\frac{t}{RC}$$
which gives
$$\ln\frac{v_c}{V} = -\frac{t}{RC}$$
and
$$v_c = V e^{-\frac{t}{RC}}$$
i.e., the capacitor voltage vC decays to zero after a period of time, the rate of decay depending on CR, which is the time constant τ.
Since $$v_R + v_c = 0$$, the magnitude of resistor voltage vR is given by:
$$v_R = V e^{-\frac{t}{RC}}$$
The negative sign is omitted intentionally because only the decaying magnitude is being shown — not its direction. Here, we’re talking about the magnitude (absolute value) of resistor voltage.
Also, since
$$i = C\frac{dv_c}{dt} = -\frac{CV}{RC} e^{-\frac{t}{RC}}$$
The magnitude of the current is:
$$i = \frac{V}{R} e^{-\frac{t}{RC}}$$
Here, the negative sign is omitted. The negative sign shows the current direction is opposite to the charging direction.
FAQs
What is a time constant in an RC circuit?
It is τ=RC. The time constant of an electrical circuit is the time required for the voltage or current to change by about 63.2% of its final steady-state value after a sudden change (such as applying or removing a voltage source).
Why does the capacitor voltage rise slowly during charging?
Because current must flow through the resistor, and the capacitor voltage builds up following an exponential law until it matches the supply.
What happens to current during charging?
It starts at a maximum (V/R) at t=0 and decays exponentially to zero as the capacitor gets fully charged.