In this topic, we have listed some of the AC Parallel circuit formulas.
For RL and RC Parallel Circuit:
| RL Parallel Circuit | 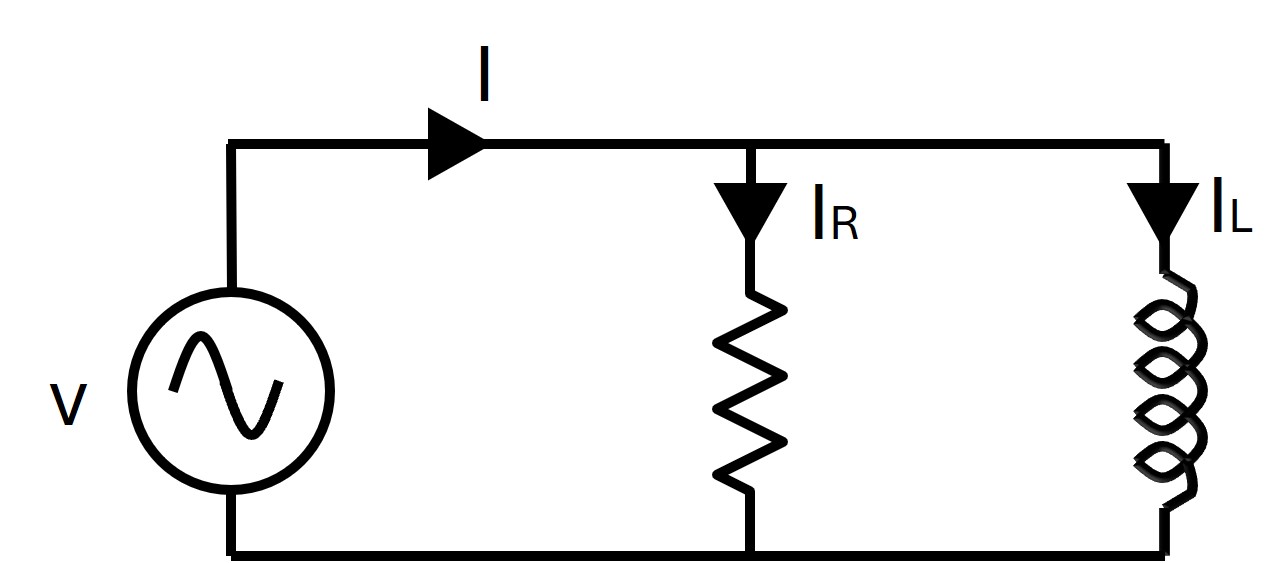 |
| RC Parallel Circuit | 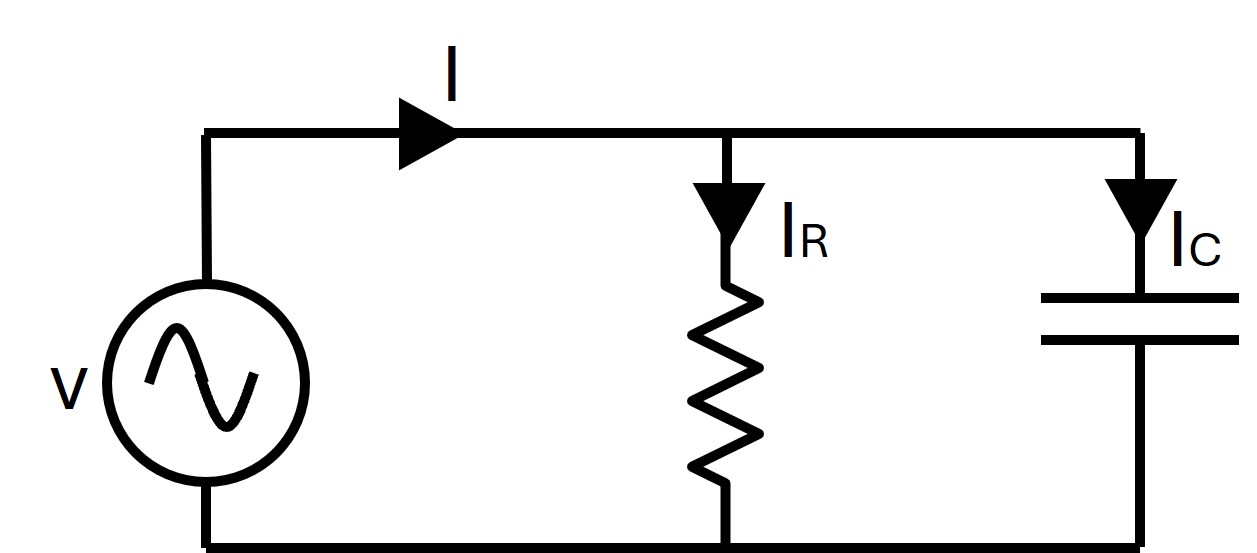 |
For RL Parallel and RC Parallel Circuit | I= Total line current IR= Current flow through the resistance IL= Current flow through the inductance IC= Current flow through the capacitance |
| For RL: For RC : | Z= Impedance R= Resistance XL= Inductive Reactance XC= Capacitive Reactance |
| For RL: For RC: | Circuit current I lags behind the applied voltage V by |
For parallel RLC Circuit:
| RLC Parallel Circuit | 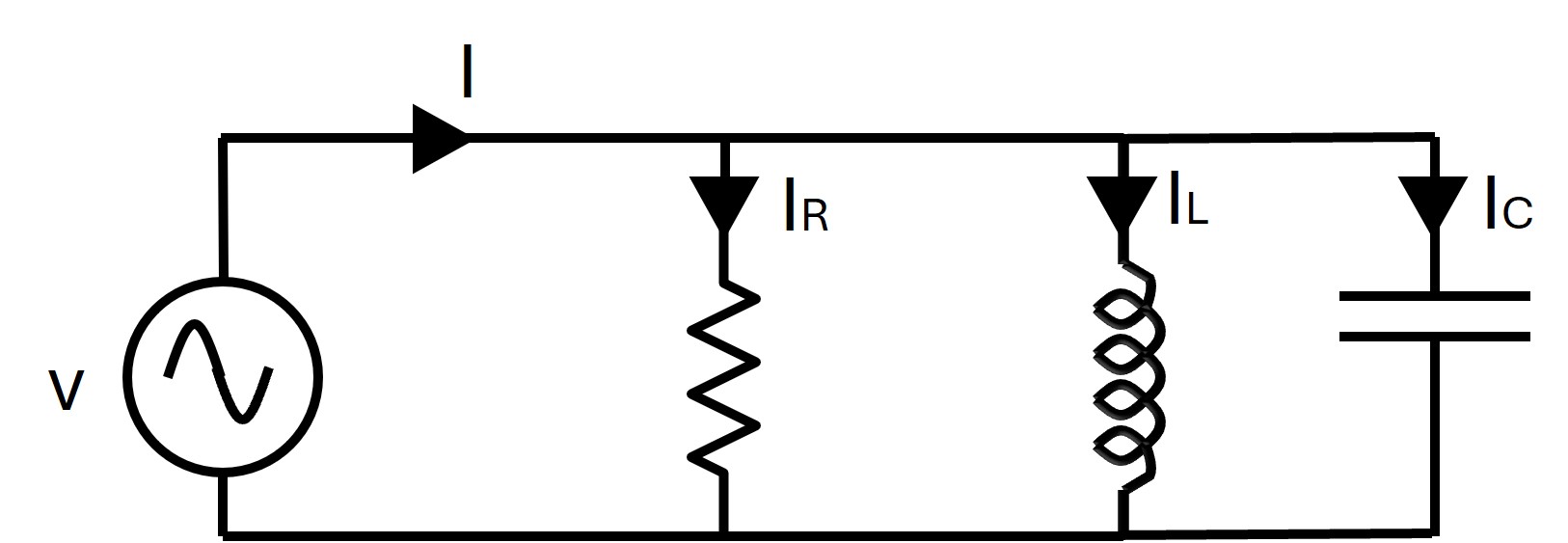 |
| For RLC Parallel: | I= Total line current IR= Current flow through the resistance IL= Current flow through the inductance IC= Current flow through the capacitance |
| For RLC Parallel: Where, | Y =Admittance G=Conductance BL=Inductive Susceptance BC= Capacitive Susceptance B= Net Susceptance= BL– BC |
| Y =Admittance G=Conductance B= Net Susceptance= BL– BC | |
| For RLC Parallel Resonance: | fr = Resonance frequency L= Inductance C= Capacitance |